
vie-magazine-sudoku
Thinking Inside the Box
The Only Complete and Comprehensive Sudoku Solution
By Sudoku Sam
We were going to spend ten days in St. Barts, so when we stopped by a pharmacy to pick up the essentials, I perused the newsstand for some interesting literature. A small Sudoku puzzle book caught my eye. “Why not?” I asked myself. After all, I know math. I even published a statistical theory article once. Not that I was really all that interested in solving puzzles—I had long since grown out of that—but it would be interesting to see how it worked. Furthermore, it was the spring of 2005, Sudoku was all the rage, and I wanted to see what it was all about. My interest, though, was in the actual solution process, not just the challenge of solving a puzzle. Besides, the cover proclaimed in French: Simple et Moyen (Easy and Moderate).
Once we had settled in at our destination, I began my first Sudoku: Simple #1. Little did I imagine that it would captivate me and forever change my life. I struggled with that little puzzle for over a week. Each day, I returned to where I had left off, and each day my frustration grew—along with my determination. “I will solve this #*@% puzzle,” I kept telling myself. “I am bigger than this.”
Finally . . . success! I had solved my first Sudoku. Still, it injured my scientific ego to think that it had taken so long, and although I had gained some insights into the process, I was still very far from understanding it. On to puzzle two—this time a Moyen. I was still working on it on the plane back to the States. My insights grew with each correct digit I placed in the matrix, but I was still far from putting it all together, and my patience was running thin. So, I went to the Internet and ordered three books on how to solve Sudoku. When they arrived, I tore into them like a hungry wolf. I didn’t really want to read them and see that someone else had figured this all out, but “Enough is enough,” I thought; I was about to throw in the towel.
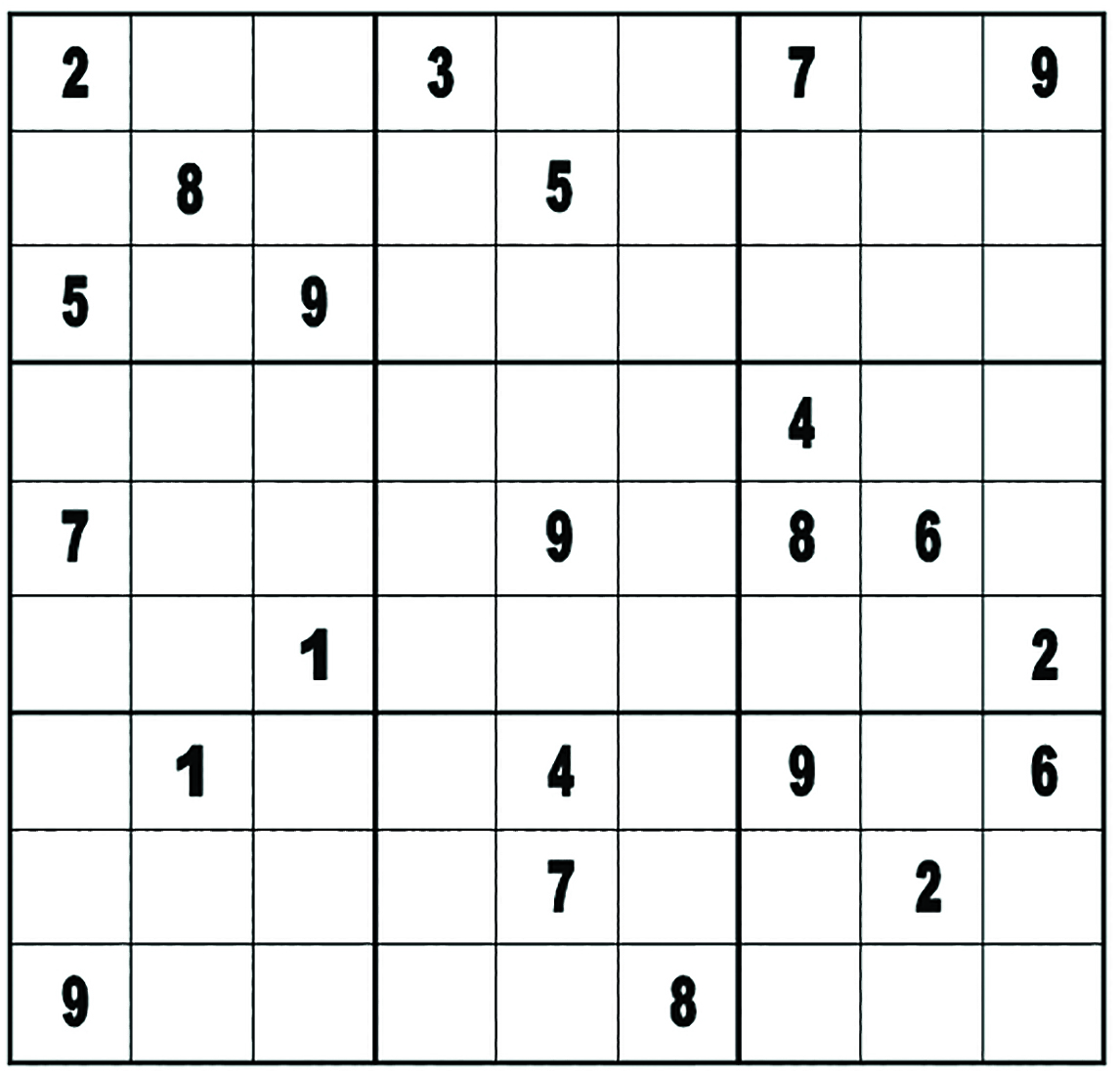
Figure 1
What I found in those three books both horrified and emboldened me. I had already formulated the rudiments of a solution strategy, and what I read offered no threat to my ideas or approach. On the contrary, I couldn’t understand why anyone would want to make the solution process even more complex! Trying to apply the books’ strategies to any given puzzle literally gave me a headache and generated massive confusion: trying to work through the logic of it was confounding. Therefore, I promised myself that I would not look at another Sudoku strategy book until I had worked through all my own thoughts on the matter. So, I started working on puzzles on WebSudoku.com and felt like I was making progress. But I was in disbelief at how fast other people were solving Sudoku on this site. I even inquired as to whether or not their time logs were real—and they were, according to the Web Sudoku folks. I plodded on.
It took about a year to put together my basic system, and I knew there were still some missing parts. I posted my findings under the title Rational Sudoku to contrast it with the other solution strategy, which I now call the “Standard Strategy”—the basis of which is known as the “Possibility Matrix.” It is a process, for those lacking a solution, in which all possible solutions are marked in each vacant cell of the matrix by placing little marks representing the missing digits. I refer to them as “digits” because they are not always numbers, and they could be replaced by letters, geometrical forms, baseball logos, etc. My grandchildren, in fact, used to solve simple Sudoku using SpongeBob SquarePants stickers. The point here: Sudoku has nothing to do with mathematics and everything to do with logic and reason. This was the appeal to me—logic and reason. Thus, what was the logic that formed the foundation of Sudoku, and how did one reason through the solution process?
“I will solve this #*@% puzzle,” I kept telling myself. “I am bigger than this.”
It seemed so simple, but to understand how to solve a Sudoku, we need to understand what a Sudoku is. Nine cells (the smallest squares) comprise each box, each row, and each column (BRC—Box-Row-Column), and each of these must contain all the digits 1 through 9. This is the “prime directive” of Sudoku. The digits provided are called “givens” and can be thought of as clues to the final (ultimate) solution. The original Sudoku was published in Dell Penny Press puzzle books in 1979. Some clever sleuthing by Will Shortz determined that the author was a retired engineer named Howard Garns, who had taken a nine-by-nine Latin square and modified it by adding additional constraints. This puzzle was called Number Place; it was literally picked up in New York in 1986 by a Japanese puzzle mogul named Maki Kaji. Since there was no copyright, Nikoli Publishing began publishing the puzzles under the awkward moniker sūji wa dokushin ni kagiru, which means “only single numbers allowed”—from whence came the name Su Doku, which means, roughly, “one number” or “single place.”
A retired jurist, Wayne Gould, discovered Sudoku while traveling in Asia. In 1999, after being rejected by the New York Times, he convinced the Times of London to publish the first “Sudoku” in English literature. The next year, the first Sudoku in the United States was published in the Boston Globe. The rest, as they say, is history. Sudoku is now the most popular puzzle in the world. It can be solved by any person of any culture, provided they understand or recognize Arabic numerals—thus, competition is open to peoples of all cultures, languages, races, and ethnicities. In fact, the winner of the first World Sudoku Championship, held in 2006, was a 31-year-old Czech woman named Jana Tylová.
The Latin square came from a popular puzzle from the Middle Ages, the “magic square,” which had deep religious significance. There is a four-by-four magic square engraved on La Sagrada Família Cathedral in Barcelona in which each row and column contains numbers that add up to thirty-three (the age of Christ when he was purportedly crucified). It is also incorporated into the emblem of the Statistical Society of Canada. In 1758, the great Swiss mathematician Leonhard Euler worked out the general solution for magic squares. Because he used Latin symbols to illustrate his solution, Euler’s formulation became known as Latin squares, which are widely used today in science and engineering. In an NxN Latin square, there must be N distinct symbols, such as the digits 1 through 9, and each symbol must occur only once in each row and once in each column.
Wei-Meng Lee first proposed the Possibility Matrix in his book, Programming Sudoku, as a last-resort method for discovering the ultimate solution of a Sudoku by computer. It was popularized by Peter Gordon, puzzle editor for Sterling Publishing Co., and Frank Longo, puzzler extraordinaire, in their book, Mensa Guide for Solving Sudoku. Gordon proposed a “new system of logic,” which he immodestly called Gordonian Logic, presumably to explain the Standard Strategy. However, the Sudoku Solution systematically unties that confusing Gordonian knot and replaces it with a true system of logic. In all fairness, you must first solve as many cells as possible before beginning to scratch your head and squirm in your seat while realizing that solutions for the remaining cells of the matrix have run out. You are stuck and know not which way to turn for the next solution. You wonder if this is a temporary “logjam” or a definitive “lockup?” This is when the Possibility Matrix is enacted, which I call the “bait and switch” moment, or, more pointedly, “the switch.” Parenthetically, there is also a little online industry that, for a nominal fee, will send you the Possibility Matrix if you send them your “locked up” matrix. You wouldn’t want to get it wrong!
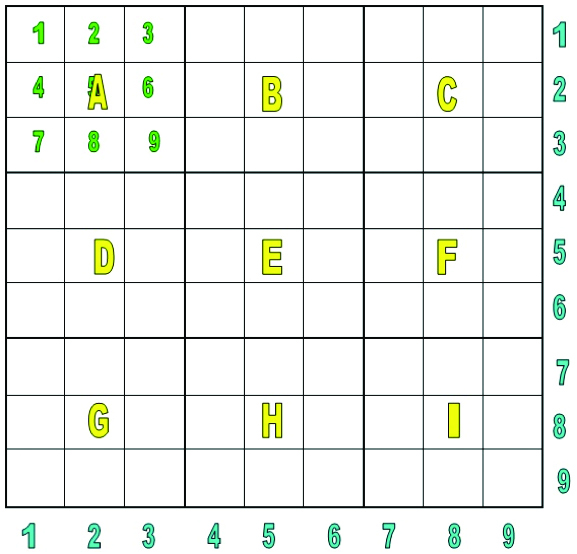
Figure 2
The Sudoku Solution uses a unique nomenclature system in the designation of cells, both within the boxes and within the matrix as a whole. This system is in stark contrast to the rigidly Cartesian approach of the Standard Strategy. The boxes are labeled with uppercase letters A through I, as shown in Figure 2. Within each box, the cells are numbered from left to right and top to bottom—as one would read Latin or Arabic texts. Rows and columns are marked with the ordinal numerals 1 through 9 from top to bottom and from left to right, respectively. Note that, here, the digits 1 through 9 represent ordered arrays, whereas, when at play in the Sudoku matrix, they lose this characteristic. Every cell is uniquely located using a single letter and a single digit, with a focus on the boxes—the component that distinguishes Sudoku.
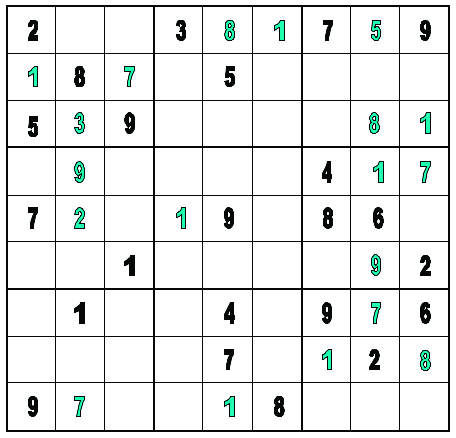
Figure 3
In Figure 3, I have worked the previous Sudoku, Figure 1, to its major logjam. Readers should work through it as well and see if they obtain the same results. You can also visit our blog, www.viezine.com/vie, and view the post titled “Thinking Inside the Box” for a comparison of the Sudoku Solution and the Standard Strategy’s Possibility Matrix. The interested reader is invited to explore the technical details of how the two strategies differ.
To sum everything up, one must ask, “Is there a best way to solve Sudoku?” There are worse ways to go than the Standard Strategy—such as the one based on roulette betting or the “sledgehammer” approach, which purports to solve Sudoku using Venn diagrams. So there must be a better strategy, and it is not the “bait and switch” act of the Standard Strategy, whose proponents do not understand the Sudoku matrix well enough to implement a cohesive plan of attack, making their solution more complex as the Sudoku becomes more difficult. Thank goodness for that, though, or I would not have had the pleasure and the sheer thrill of discovery in developing what I believe is the best way to solve Sudoku: the Sudoku Solution. Starting out with the Sudoku Solution will save you a lot of time, aggravation, confusion, and anxiety—as stated in the title of my starter’s book: Sudoku Sam’s Starting Out Right Strategy for Solving Sudoku.
My strategy is presented in its entirety in a three-volume set, available for $19.99. To purchase, you can contact Sudoku Sam at skiplantz@hotmail.com, go to Amazon.com, or visit Sundog Books in Seaside, Florida. Along with the above title, the collection includes Sudoku Sam’s No Notes Strategy for Solving Sudoku and Sudoku Sam’s Meta-Strategy for Solving Sudoku. I am currently bringing the three tomes together into my definitive book: The Only Complete and Comprehensive Sudoku Solution. Contact me at the above e-mail to sign up for Sudoku updates and prepublication offers. Meanwhile, buying the current set of Sudoku Sam’s guides will automatically get you the definitive book for free when it goes to press!
Thinking inside the box,
Sudoku Sam
— V —
Share This Story!
KEEP UP WITH THE LATEST STORIES FROM VIE
















































































































































